ABER!
Ebenso wie bei der Schallplatte bildet die Spur einer CD eine Spirale, die allerdings in der Mitte beginnt. Wenn man nun wüsste, welchen Abstand diese Spuren von einander haben, dann könnte man die Frage durch eine einfache Rechnung beantworten.
Ein Versuch aus der Wellenoptik bringt einen ersten Hinweis (OK, das geht über den Realschulstoff deutlich hinaus, ist aber dennoch interessant und hoffentlich auch verständlich!).
Die Spuren einer CD wirken wie die Linien eines optischen Gitters. Das ist, trivial gesagt, vergleichbar mit einem Lattenzaun durch den Sonnenlicht fällt. Durch die Lücken im Zaun wird ein dickes Lichtbündel in viele einzelne dünne Lichtbündel zerlegt, die ihrerseits, wie punktförmige Lichtquellen wirken, also Licht nach allen Seiten ausstrahlen. Betrachtet man das Licht als elektromagnetische Welle, dann gibt es in Ausbreitungsrichtung Berge und Täler, die einander abwechseln. Die Wellenlänge ergibt sich, wenn man einen Wellenberg und ein Tal hinter einander setzt. Punkte gleicher Phasenlage erreicht man, wenn man in Ausbreitungsrichtung um eine Wellenlänge weiterschreitet (Fig.1a/b).
Kommen an einer Stelle die Wellen zweier Quellen zusammen, dann gibt es eine Überlagerung. Wenn die beiden Wellen einen Phasenunterschied von einer halben Wellenlänge = λ/2 haben, trifft ein Berg auf ein Tal, die Amplituden löschen sich gegenseitig aus - es herrscht an dieser Stelle Dunkelheit (Fig 1b). Kombinieren die Wellen aber so, dass Berg auf Berg oder Tal auf Tal trifft, dann gibt es Verstärkung und die Stelle erscheint hell, es entsteht ein Helligkeitsmaximum. Die Bedingung für Maxima ist also, dass die Wellen einen Gangunterschied (=Phasenverschiebung) von einer ganzen Wellenlänge λ haben (Fig. 1a). Die folgenden Skizzen verdeutlichen das.
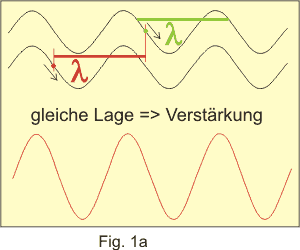
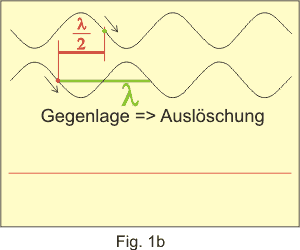
Die feinen Linien der CD wirken als "Kratzer" in der Oberfläche wie die Zaunlatten. Durch die Stellen dazwischen kann Licht fallen. Der Strahl von einem Laserpointer ersetzt das Sonnenlicht beim Lattenzaun. Durch das optische Gitter wird das Laserlichtbündel in viele feine Einzelbündel zerlegt, die alle für sich als einzelne Lichtquellen wirken und sich nach obigen Überlegungen überlagern können. Die Grundlagen für meinen Versuch hat übrigens vor ca. 350 Christiaan Huygens formuliert.
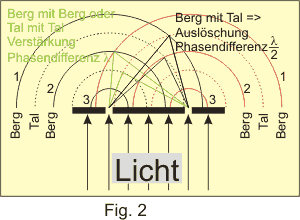
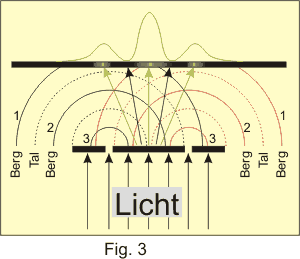
Figur 2 zeigt den Ausschnitt eines optischen Gitters. An den Spaltöffnungen breiten sich Elementarwellen in der Ebene als konzentrische Halbkreise aus. Durch Überlagerung (Interferenz) entstehen auf dem Schirm helle und dunkle Bereiche, je nachdem welche Teile der Wellen dort zusammenkommen.
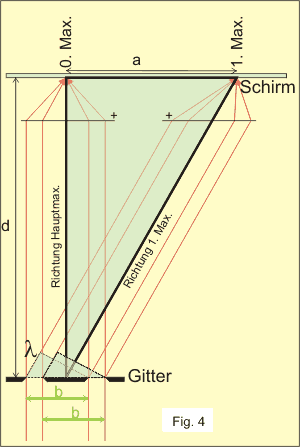
Mein Versuchsaufbau entspricht der Figur 4. Als Gitter verwendete
ich zunächst eines mit bekannter Gitterkonstante
g = 13400 Linien / inch = 527,56 Linien / mm.
Das entspricht einem errechneten Linienabstand
b = 1,900 µm.
Der Verwendete Laserpointer hat eine bekannte Wellenlänge von λ
= 532 nm. Ich wollte zunächst herausfinden, wie genau die Ergebnisse sein
werden, die aus der Anordnung resultieren.
Ein bisschen 9.-Klassmathematik:
 Die grauen
Dreiecke in Fig. 4 sind zueinander ähnlich. Mit dem sws-Ähnlichkeitssatz
und dem Satz von Pythagoras im großen Dreieck gilt:
Die grauen
Dreiecke in Fig. 4 sind zueinander ähnlich. Mit dem sws-Ähnlichkeitssatz
und dem Satz von Pythagoras im großen Dreieck gilt:
Mit den ersten Messwerten
d = 18,0 cm
a = 5,25 cm
λ = 532 nm
ergibt sich ein Linienabstand des optischen Gitters zu b = 1,90 • 103
nm = 1,90 µm was will man mehr?
In der Messeinrichtung Abb.1 kann man die eingespannte CD und den Laserpointer sehen. Die CD ist eine der Scheiben, die oft den Stapel beim Kauf oben und unten als Kratzschutz abschließen. Vorteil ist ganz klar die fehlende Verspiegelung. Die zukünftigen Spuren sind aber schon angelegt, wie sich zeigen wird, auch die Lands und Pits des geplanten Inhalts.
 Abb. 1: Der Versuchsaufbau zu den Beugungsversuchen. Zur Entfernung der
Vorderkante vom Schirm sind noch 1,5cm zu addieren, denn die Entfernung d wird
ab der CD gemessen. Wenn d groß genug ist, spielt es auch keine Rolle
mehr, ob die Spurseite oder die glatte Seite der CD zum Schirm weist.
Abb. 1: Der Versuchsaufbau zu den Beugungsversuchen. Zur Entfernung der
Vorderkante vom Schirm sind noch 1,5cm zu addieren, denn die Entfernung d wird
ab der CD gemessen. Wenn d groß genug ist, spielt es auch keine Rolle
mehr, ob die Spurseite oder die glatte Seite der CD zum Schirm weist.
Wie im Vorversuch will ich den Abstand der Gitterlinien = Spuren ermitteln. Es sind also die gleichen Messungen erforderlich - es wird auch genau so gerechnet.
 Abb.
2: Die erste Messung läuft. Deutlich zu erkennen sind das Hauptmaximum
in der Mitte und die beiden ersten Nebenmaxima.
Abb.
2: Die erste Messung läuft. Deutlich zu erkennen sind das Hauptmaximum
in der Mitte und die beiden ersten Nebenmaxima.
 Abb.3:
Die Ablesung bringt einen Wert von 12,7 cm für die Entfernung a des
ersten Nebenmaximums zum Hauptmaximum in der Mitte. Die Vorderkante des Apparats
stand 32,0cm vor dem Schirm, für d ergibt sich somit d = 33,5cm. Deutlich
zu sehen ist auch, dass das Maximum vertikal gestreckt ist. Bei dem optischen
Gitter des Orientierungsversuchs waren auch die Nebenmaxima punktförmig.
Ich gehe davon aus, dass auch die Lands und Pits der Spur das Laserlicht ablenken
wodurch der Strich entsteht.
Abb.3:
Die Ablesung bringt einen Wert von 12,7 cm für die Entfernung a des
ersten Nebenmaximums zum Hauptmaximum in der Mitte. Die Vorderkante des Apparats
stand 32,0cm vor dem Schirm, für d ergibt sich somit d = 33,5cm. Deutlich
zu sehen ist auch, dass das Maximum vertikal gestreckt ist. Bei dem optischen
Gitter des Orientierungsversuchs waren auch die Nebenmaxima punktförmig.
Ich gehe davon aus, dass auch die Lands und Pits der Spur das Laserlicht ablenken
wodurch der Strich entsteht.
Die Berechnung:
d = 33,5 cm Nachdem die vorherbereitende
Messung so genau ausfiel, gibt es keinen triftigen Grund an der Genauigkeit dieser
Messung zu zweifeln. Trotzdem - beim Nachlesen im Web findet man Werte von 1,6
µm als Spurabstand. Wo steckt der Fehler?
Nachdem die vorherbereitende
Messung so genau ausfiel, gibt es keinen triftigen Grund an der Genauigkeit dieser
Messung zu zweifeln. Trotzdem - beim Nachlesen im Web findet man Werte von 1,6
µm als Spurabstand. Wo steckt der Fehler?Eine weitere transparente Abdeckscheibe wird gesucht und eingesetzt.
Sie ist höchstens halb so dick wie die erste und liefert auch ein noch
merkwürdigeres Ergebnis: λ = 0,74 µm. Das Messobjekt war demnach
keine CD sondern die eine Hälfte einer doppelseitigen DVD von 0,6 mm Dicke
und einem korrekten Spurabstand von 0,74 µm. Erst die dritte Messung mit
einem normalen CD-Rohling lieferte im Reflexverfahren nach einem marginalen
Umbau der Messeinrichtung mit d=42,5cm und einem Abstand der ersten Nebenmaxima
2a=31cm mit dem grünen Laser einen besseren Wert für den Spaltabstand
b=1,55µm. Von einem identischen zweiten Rohling wurde nun mit einem scharfen
Messer die Silberschicht angeritzt und durch kräftiges Blasen entfernt.
Eine 4. Messung brachte für diese Scheibe sowohl im Durchlicht- wie im
Reflexverfahren den selben Wert.
In einer interessanten Rechnung ergibt sich die Gesamtlänge der CD-Spur zu ungefähr 6 km.

Fig 7: Spurlänge der CD
Abschließend wollte ich wissen, welche Wellenlänge meine beiden roten Laser haben. Also fix in die Messanordnung eingebaut und die Werte bestimmt.
Abstand der Nebenmaxima: 2a = 36,6 cm
bereinigter Abstand vom Schirm: d = 40,0 cm
Gitterabstand : 1,55 µm

Fig. 8: Wellenlänge eines roten Laserspointers
Mit dem optischen Gitter aus dem Orientierungsversuch erhalte ich glatte 650 nm. Für den zweiten etwas helleren roten Laserpointer ergeben sich 632 nm.
Bei DLP-Beamern (Digital Light Processing) lenkt ein Array von kleinen Spiegelchen das Licht der Lampe, nachdem es das Farbrad passiert hat, in Richtung Optik und Projektionsfläche. Die kleinen Spiegelchen sind in Zeilen und Spalten angeordnet und - sehr klein.
Vor einiger Zeit bekam ich einen Optoma mit defektem Spiegelarray in die Finger. Netzteil, Hochspannungseinheit und Lampe waren noch OK, weswegen ich diese Teile zum Bau Scheinwerfers ausgebaut habe. Das Spiegelarray lag lange Zeit unbeachtet im Keller rum, bis ich zufällig mal mit einem Laserpointer draufleuchtete. Der "Sternenhimmel" verblüffte mich anfangs, dann kam aber schnell das Aha: das Spiegelarray ist ein zweidimensionales Gitter, natürlich muss dann auch das Interferenzmuster zweidimensional sein. Einen ähnlichen Effekt kann beobachten, wenn man nachts mit einem Regenschirm unterwegs ist. Die die Lichter von engegenkommenden Autos erscheinen dann durch den feinmaschigen Schirmstoff auch zu so einem Muster aufgespalten.

Das DLP-Array 1076-6319W

schräg von unten mit einem 532nm-Laser angestrahlt

liefert diesen Sternenhimmel
Spiegelarray und Schirm waren genau 100,0cm voneinander entfernt, die Interferenzpunkte haben 5,0cm Abstand. Mit den Formeln der Fig. 6errechnet sich ein Spiegelabstand von 10,6 µm. Die Struktur ist also 10 mal gröber wie die einer CD oder gar DVD. Wenn man allerdings bedenkt, dass jedes Spiegelchen, halb so dick wie ein Haar auch noch gezielt bewegt werden muss, dann ist diese Technik schon bewundernswert.
Ach ja - wie viele Spiegelchen sind denn nun auf dem Chip? Das Interferenzmuster sagt uns, dass vertikale und horizontale Abstände gleich sind. Die Breite des Chips ist 11,5mm, seine Höhe 8,6mm, horizontal passen daher 11,5E-3 m / 10,6E-6 m = 1084 in die Zeile und hochgerechnet 813 in die Spalte, macht die läppische Summe von 0,88 Millionen Spiegelchen auf einer Fläche von knapp 1cm².
Hier habe ich auch noch ein Foto von der Chipoberfläche in 200-facher Vergrößerung unter dem Mikroskop aufgenommen. Man kann die Struktur erahnen. Die 5 hellen Punkte im Zentrum sind defekte Pixel, die dazu geführt haben, dass das Gerät ausgemustert wurde. Das natürlich nicht nur wegen der 5 Dinger (einer Breite von ca 50 Spiegelchen im Bild entsprechend ca. 530µm) sondern wegen der Unzahl weiterer auf dem gesamten Chip. Je nach festgefahrener Richtung gab es im Bild schwarze und weiße "Ameisen" in der Projektion.

Struktur der Chipoberfläche des 1076-6319W